Creating the Bolt Compiler: Part 4
An accessible introduction to type theory and implementing a type-checker
June 15, 2020
11 min read
Last updated: January 13, 2021
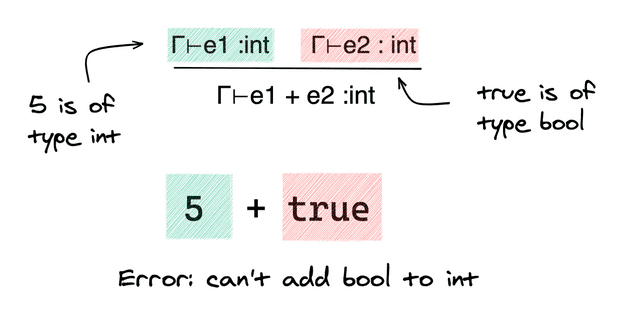
This post is split into 2 halves: the first half explains the theory behind type-checkers, and the second half gives you a detailed deep-dive into how it’s implemented in our compiler for our language Bolt. Even if you aren’t interested in writing your own language, the first half is useful if you’ve ever heard about type systems and want to know how they even work!
Share This On Twitter
If you find this useful, please share this on Twitter. I'm writing up posts on implementing generics and inheritance in this language too!

What are types?
We’d discussed this briefly in the first part of the compiler series, however let’s revisit this:
Types are a way of grouping program values based on the behaviour we’d like them to have. We have our own “types” in our day-to-day lives. E.g. grouping people as adults and children.
Grouping values together means the compiler doesn’t have as many cases to handle. It means we don’t need to look at the actual value, we just reason about it based on the group it’s in (its type).
E.g. the values 0, 1, 2, 3… and all other integers are all given the type int. Values of type int can take part in arithmetic operations like multiplication on them but we can’t concatenate them (like strings). See how the type (int vs string) defines the behaviour of the value (what we can do with them)?
It’s even clearer in our custom types. E.g when you define a custom Animal class with eat() and sleep() methods, you’re saying that objects of type Animal have eat and sleep behaviour. But we can’t divide two Animal objects by each other - that’s not the behaviour we’d allow. What would dog / cat even mean?
The role of the type-checker is to prevent this kind of nonsensical behaviour from happening. That’s what we’re building today.
All practical languages have type-checking in some form. Statically typed languages like Rust, Java or Haskell check the types at compile-time. Dynamically-typed languages like JS and Python do still have types - values are tagged with types at runtime, and they check types when executing. If you try to run 5 / "Hello", it won’t actually run the code, JS/Python will see "Hello has type string and will throw a runtime error instead of executing it.
Right now, this all feels a little hand-wavey. Let’s formalise “preventing nonsensical behaviour”. We want a list of rules to check a program against, and then if it passes those, we know our program is safe.
This collection of rules is called a type system.
Type Systems
Here’s the deal: types define safe behaviour. So if we can give an expression a type, we can use its type to make sure it’s being used in the correct way. The type system’s rules (called typing judgements) therefore try to assign a type to an expression .
We start by defining seemingly obvious facts, like true is of type bool. In our type system, the rule is written as follows:
Don’t be scared by the maths notation: means “it follows that”. You can read this as “it follows that the expression true has type bool. In general, can be read as “it follows that expression e has type t”.
Here’s a couple more obvious facts.
for any integer .
Typing environments
Thing is, looking at an expression on its own isn’t always enough for us to type-check it. What’s the type of a variable x? What should we put in place of the ? below?
Well it depends on what type it was given when it was defined. So when type-checking, we’ll need to keep track of the variables’ types as they are defined. We call this the typing environment, represented in our rules as . Think of as a look-up function that maps variables to their types.
We update our typing rules to include :
.
Back to our typing rule here:
If , then we can say that:
.
In our typing rules we stack these two statements to give one compound typing rule for variables. This is an example of an inference rule.
Inference rules
This odd stacked “fraction” is a way of representing deductive reasoning (like Sherlock Holmes!). If everything on the top holds, then we infer the bottom also holds.
Here’s another rule. This says that if we know and are ints, then if we add them together the result is also an int.
Using these inference rules, we can stack together our pieces of evidence about different parts of the program to reason about the whole program. This is how we build up our type system - we stack our rules.
Let’s combine what we’ve learnt so far to type-check a little expression: x + 1 where our environment tells us x is an int.
Now if it turns out x is an string, then doesn’t hold, so all the rules stacked below it don’t hold. Our type-checker would raise an error, as the types don’t match up!
Axioms
It’s convention here to represent the facts (axioms) with a line above them. You can think them as the “base case”:
Since they have nothing on the top, technically everything on the top is true. So the bottom always holds.
If you look back to our example and flip it upside down, it kind of looks like a tree. It also lays out our reasoning, so acts as a proof - you can just follow the steps. Why is x+1 an int? Well x and 1 are ints? Why is x an int? Because… You get the idea. So what we’ve constructed here is called a proof tree.
Okay, let’s look at another rule. What about an if-else block?
if (something) {do_one_thing} else {do_something_else}
Well, the something has to have type bool as it’s a condition. What about the branches? We need to give this expression an overall type, but because we’re statically type-checking, we don’t know which branch will be executed at runtime. Therefore we need both branches to return the same type (call it ), so the expression has the same type regardless of which branch we execute.
JavaScript and Python would allow different types for each branch, since they’re doing their type-checking at runtime (dynamically typed), so they know which branch was chosen.
Typing the Overall Program
This post would end up being too long if I were to list all the rules, but you can work through each of the cases. We look at the grammar we defined in the previous post and write the corresponding rules.
We want to show the program is well-typed (you can assign it a type) to show it is safe. So we essentially want a proof tree that shows it has some type (we don’t care which):
There’s just one thing missing here. Initially - it’s empty as we haven’t defined any variables. How do we add variables to ?
Remember, we add variables to as we declare them in our program. The syntax for this is a let declaration. So say we have the following program:
// we have some gammalet x = e1// update gamma with x's type// continue type-checkinge2
We type-check this in the order the program executes:
- We get the type of the expression , call it
- We then extend the environment with the new mapping .
- We use this extended environment (which we write as ) to type-check and give it type .
The whole typing rule thus looks like:
Type Checking vs Type Inference
One finer point: here we wrote let x = e. We could have equally written this as let x : t = e - where the programmer annotates x with type t. e.g. let x : int = 1 + 2.
These lead to different typing algorithms - in the first case the compiler infers that 1+2 has type int, and in the second case, the compiler has to check that 1+2 has type int (since we specified the type int of x).
As you might imagine, type inference means that the programmer has to write fewer type annotations, but it is much more complex for the compiler - it’s like filling a Sudoku from scratch versus checking a Sudoku solution is valid. OCaml and Haskell are examples of languages with type inference baked in.
In practice, most statically-typed languages do require some type annotations, but can infer some types (e.g. the auto keyword in C++). This is like completing a partially solved Sudoku puzzle and is much easier.
For Bolt, we’re going to infer types within a function or method definition, but require programmers to annotate the parameter and return types. This is a nice middle ground.
function int something(int x, bool y){let z = ... // z's type is inferred...}
Okay, enough theory, let’s get to implementing this type-checker!
Implementing a Type-checker
Just give me the code!
You’ll need to clone the Bolt repository:
git clone https://github.com/mukul-rathi/bolt
The Bolt repository master branch contains a more complex type-checker, with support for inheritance, function/method overloading and generics. Each of these topics will get its own special post later in the series.
So instead, you’ll want to look at the simple-compiler-tutorial release. You can do this as follows:
git checkout simple-compiler-tutorial
This contains a stripped-back version of Bolt from earlier in the development processs. (View this online)
The folder we care about is src/frontend/typing.
A note on OCaml syntax
In this tutorial we’ll be using OCaml syntax. If you’re unfamiliar with this, the main gist is that we’ll:
a) Pattern match each of the cases (like switch statements in other languages). Here we have a variable x and we do different things based on each of its cases A, B
match x with| A -> something| B -> something_else
b) Use a Result monad: in essence, this has two values: Ok something and Error. We sequence each of the operations using the >>= operator - you don’t need to know anything about monads for this tutorial, just think of this as the same as normal expression sequencing with ;s, just that we’re using another operator to represent that earlier expressions might raise an error.
Types in Bolt
Bolt has four main types: int, bool, void and user-defined classes. We represent these four options using a variant type type_expr in OCaml:
type type_expr = TEInt | TEClass of Class_name.t | TEVoid | TEBool
Annotating our AST with types
Let’s recap our Abstract Syntax Tree from the last part of the series:
type identifier =| Variable of Var_name.t (* x *)| ObjField of Var_name.t * Field_name.t (* x.f *)type expr =| Integer of loc * int (* 1, 2 *)| Boolean of loc * bool (* true*)| Identifier of loc * identifier| Constructor of loc * Class_name.t * constructor_arg list (* new Class(args)*)| Let of loc * type_expr option * Var_name.t * expr(** let x = e (optional type annotation) *)| Assign of loc * identifier * expr| If of loc * expr * block_expr * block_expr(** If ___ then ___ else ___ *)...and block_expr = Block of loc * expr list
This AST annotates each expression with loc - the line and position of the expression. In our type-checking phase, we’ll be checking the types of each of the possible expressions. We’ll want to store our results by directly annotating the AST, so the next compiler stage can view the types just by looking at the AST.
This AST gets the imaginative name typed_ast:
type identifier =| Variable of type_expr * Var_name.t| ObjField of Class_name.t * Var_name.t * type_expr * Field_name.t(** class of the object, type of field *)type expr =| Integer of loc * int (** no need to annotate as obviously TEInt *)| Boolean of loc * bool (** no need to annotate as obviously TEBool *)| Identifier of loc * identifier (** Type info associated with identifier *)| Constructor of loc * type_expr * Class_name.t * constructor_arg list| Let of loc * type_expr * Var_name.t * expr| Assign of loc * type_expr * identifier * expr| If of loc * type_expr * expr * block_expr * block_expr(** the If-else type is that of the branch exprs *)...and block_expr =| Block of loc * type_expr * expr list (** type is of the final expr in block *)
We don’t annotate obvious types, like for Integer and Boolean, but we annotate the type of the overall expression for other expressions e.g. the type returned by an if-else statement.
A good rule of thumb when annotating the AST is, what would the next stage need to be told about the program that it can’t guess from it being well-typed? For an if-else statement, if it is well-typed then the if-condition expression is clearly of type bool, but we’d need to be told the type of the branches.
The Type Environment
Recall that we used our type environment to look up the types of variables. We can store this as a list of bindings (variable, type) pairs.
type_env.ml also contains a “environment” of helper functions that we’ll use in this type-checking phase. These are mostly uninteresting getter methods that you can look at in the repo.
type type_binding = Var_name.t * type_exprtype type_env = type_binding list(** A bunch of getter methods used in type-checking the core language *)val get_var_type : Var_name.t -> type_env -> loc -> type_expr Or_error.t...
It also includes a couple of functions that check we can assign to an identifier (it’s not const or the special identifier this) and that check we don’t have duplicate variable declarations (shadowing) in the same scope. These again are conceptually straightforward but are necessary just to cover edge cases.
For example:
let check_identifier_assignable class_defns id env loc =let open Result inmatch id with| Parsed_ast.Variable x ->if x = Var_name.of_string "this" thenError(Error.of_string(Fmt.str "%s Type error - Assigning expr to 'this'.@." (string_of_loc loc)))else Ok ()| Parsed_ast.ObjField (obj_name, field_name) ->get_obj_class_defn obj_name env class_defns loc>>= fun class_defn ->get_class_field field_name class_defn loc>>= fun (TField (modifier, _, _, _)) ->if modifier = MConst thenError(Error.of_string(Fmt.str "%s Type error - Assigning expr to a const field.@."(string_of_loc loc)))else Ok ()
Typing Expressions
This. This is the crux of the implementation. So if you’ve been skimming the post, here’s where you should pay attention.
What do we need to type-check an expression?
We need the class definitions and function definitions, in case we need to query the types of fields and function/method type signatures. We also need the expression itself, and the typing environment we’re using to type-check it.
What do we return? The typed expression, along with its type (we return type separately to make recursive calls more straightforward). Or we return an error, if the expression is not well-typed.
Our function type signature captures this exactly:
val type_expr :Parsed_ast.class_defn list-> Parsed_ast.function_defn list-> Parsed_ast.expr-> type_env-> (Typed_ast.expr * type_expr) Or_error.t
In the second post in this series, I discussed why we’re using OCaml. This stage of the compiler is one where it really pays off.
For example to type an identifier, we pattern match based on whether it is a variable x or an object field x.f. If it is a variable then we get its type from the environment (we pass in loc as line+position info for error messages). If it returns a var_type without an error, then we return the type-annotated variable.
If it is an object field x.f, then we need to look up the type of object x in the env and get its corresponding class definition. We can then look up the type of field f in the class definition. Then we annotate the identifier with the two bits of type information we’ve just learnt: the class of the object, and the field type.
Our code does exactly that, with no boilerplate:
let type_identifier class_defns identifier env loc =let open Result inmatch identifier with| Parsed_ast.Variable var_name ->get_var_type var_name env loc>>| fun var_type -> (Typed_ast.Variable (var_type, var_name), var_type)| Parsed_ast.ObjField (var_name, field_name) ->get_obj_class_defn var_name env class_defns loc>>= fun (Parsed_ast.TClass (class_name, _, _, _) as class_defn) ->get_class_field field_name class_defn loc>>| fun (TField (_, field_type, _, _)) ->(Typed_ast.ObjField (class_name, var_name, field_type, field_name), field_type)
Right, so let’s look at expressions. This again is clean code that just reads like our typing judgements. We have expr1 binop expr2 where expr1 and expr2 are being combined using some binary operator e.g. +.
Let’s remind ourselves of the rule:
What did this say? We type-check the subexpressions and first. If they’re both ints then the overall expression is an int.
Here’s the main conceptual jump: type-checking each of the expressions on the top of the judgements corresponds to recursively calling our type-checking function on the subexpressions. We then combine the results of these type-checking judgments using our rule.
So here, we type-check each of the subexpressions expr1 and expr2 (type_with_defns just makes the recursive call shorter).
let rec type_expr class_defns function_defns (expr : Parsed_ast.expr) env =let open Result inlet type_with_defns = type_expr class_defns function_defns inlet type_block_with_defns = type_block_expr class_defns function_defns in match expr with| Parsed_ast.BinOp (loc, bin_op, expr1, expr2) -> (type_with_defns expr1 env>>= fun (typed_expr1, expr1_type) ->type_with_defns expr2 env>>= fun (typed_expr2, expr2_type) ->
Recursive calls, check.
Next, because our code deals with more binary operators than just + we slightly generalise our typing judgement. Regardless of whether it is && + or >, the operands expr1 and expr2 have to have the same type. Then we check that this type is int for the + * / % arithmetic operator cases.
If so, then all Ok and we return TEInt as the type of the operand.
if not (expr1_type = expr2_type) thenError ... (* can't have different types *)elselet type_mismatch_error expected_type actual_type = ...match bin_op with| BinOpPlus | BinOpMinus | BinOpMult | BinOpIntDiv | BinOpRem ->if expr1_type = TEInt thenOk (Typed_ast.BinOp (loc, TEInt, bin_op, typed_expr1, typed_expr2), TEInt)else type_mismatch_error TEInt expr1_type...
As another example of a binary operator, let’s look at < <= >>> >=. These take in integers and return a bool, so we check that the operand expr1 has type TEInt and we return TEBool
| BinOpLessThan | BinOpLessThanEq | BinOpGreaterThan | BinOpGreaterThanEq ->if expr1_type = TEInt thenOk (Typed_ast.BinOp (loc, TEBool, bin_op, typed_expr1, typed_expr2), TEBool)else type_mismatch_error TEInt expr1_type
Ok, still with me? This post is getting long, so let’s just look at if-else statements and let expressions, and then you can look at the rest of the code in the repo.
Again, let’s remind ourselves of our typing judgement for if-else.
That’s three expressions on top of the inference rule.
What do these expressions correspond to? Say it with me, recursive calls!
| Parsed_ast.If (loc, cond_expr, then_expr, else_expr) -> (type_with_defns cond_expr env>>= fun (typed_cond_expr, cond_expr_type) ->type_block_with_defns then_expr env>>= fun (typed_then_expr, then_expr_type) ->type_block_with_defns else_expr env>>= fun (typed_else_expr, else_expr_type) ->
Now we need to check that the returned types are what we expected, i.e. the branches have the same type, and the condition expression has type TEBool. If that’s the case, it’s all Ok and we can return the type of the branch.
if not (then_expr_type = else_expr_type) thenError ...elsematch cond_expr_type with| TEBool ->Ok( Typed_ast.If(loc, then_expr_type, typed_cond_expr, typed_then_expr, typed_else_expr), then_expr_type )| _ ->Error ...
Right, final expression for this post, the let expression, which looks like this:
Again, this requires two recursive calls, but note that the second typing judgement requires the type of the first - we need to pass in an extended type environment (after we type-checked ) to account for this.
We also have an additional requirement: we want our let expressions to be block-scoped.
if {let x = ...// can access x here} else {// shouldn't be able to access x here}// or here
So in essence, we want to only update the environment
- if we have a
letexpression, - only for subsequent expressions in the block
We can encode this by pattern-matching on our block type-checking rule. If there are no subsequent expressions (i.e. we have no expressions (pattern-match on []) or just one expression (pattern-match on [expr]) in the block), then we don’t need to update our environment.
type_block_expr class_defns function_defns (Parsed_ast.Block (loc, exprs)) env =...>>= fun () ->match exprs with| [] -> Ok (Typed_ast.Block (loc, TEVoid, []), TEVoid) (* empty block has type void *)| [expr] ->type_with_defns expr env>>| fun (typed_expr, expr_type) ->(Typed_ast.Block (loc, expr_type, [typed_expr]), expr_type)
Only if we have at least two expressions left in our block (pattern-match on expr1 :: expr2 :: exprs), and the first of the two is a let expression do we update the environment for the rest of the block. We use this updated environment in a recursive call on expr2::exprs (the remaining expressions). We then combine the result of the typed blocks.
| expr1 :: expr2 :: exprs ->type_with_defns expr1 env>>= fun (typed_expr1, expr1_type) ->(let updated_env =match typed_expr1 with| Typed_ast.Let (_, _, var_name, _) -> (var_name, expr1_type) :: env| _ -> env intype_block_with_defns (Parsed_ast.Block (loc, expr2 :: exprs)) updated_env)>>| fun (Typed_ast.Block (_, _, typed_exprs), block_expr_type) ->(Typed_ast.Block (loc, block_expr_type, typed_expr1 :: typed_exprs), block_expr_type)
Typing Class and Function Definitions
We’ve broken the back of the type-checking now. Let’s just wrap up by checking class and function definitions.
We’ll skip over the tedium of checking that there are no duplicate class definitions or duplicate field definitions in a class etc. (this is in the repo). Likewise, checking that the types annotated in fields and method/function type signatures are valids is just a matter of checking there is a corresponding class definition.
Unlike our main function, for other functions, we don’t actually start with an empty environment when type-checking the function body as we already know the types of some variables - the parameters to the function!
let init_env_from_params params =List.map~f:(function TParam (type_expr, param_name, _, _) -> (param_name, type_expr))params...type_block_expr class_defns function_defns body_expr(init_env_from_params params)
We also need to check that the type of the result of the body is the return type (or if it is void then we don’t care about the type returned).
>>= fun (typed_body_expr, body_return_type) ->(* We throw away returned expr if return type is void *)if return_type = TEVoid || body_return_type = return_type thenOk(Typed_ast.TFunction(func_name, maybe_borrowed_ret_ref, return_type, params, typed_body_expr))else Error ...
For class methods, we can initialise the environment and check the return type in the same way. But we know the type of another special variable this - the class itself.
let init_env_from_method_params params class_name =let param_env =List.map~f:(function TParam (type_expr, param_name, _, _) -> (param_name, type_expr))params in(Var_name.of_string "this", TEClass class_name) :: param_env```
Where does this fit in the Bolt pipeline?
We’re two stages into the Bolt compiler pipeline - seen in the compile_program_ir function.
let compile_program_ir ?(should_pprint_past = false) ?(should_pprint_tast = false)?(should_pprint_dast = false) ?(should_pprint_drast = false)?(should_pprint_fir = false) ?(ignore_data_races = false) ?compile_out_file lexbuf =let open Result inparse_program lexbuf>>= maybe_pprint_ast should_pprint_past pprint_parsed_ast>>= type_program>>= maybe_pprint_ast should_pprint_tast pprint_typed_ast>>= ...
Take Away: 3 Actionable Steps
If you’ve got this far, amazing job! The Bolt repo contains the full code listing with all the typing judgements for each case of the compiler.
Let’s recap what we’ve done so far:
- Define what properties in your expression you want to type-check. E.g. a condition expression has type
bool. - Formalise this with a typing judgement. Use the inference rule to reason about subexpressions.
- Map the subexpressions in the inference rule to recursive calls, then use the inference rule to combine their results.
Next up, we’ll talk about the dataflow analysis used to type-check our linear capabilities in Bolt. This is similar to how the Rust borrow checker uses “non-lexical lifetimes” to check borrowing.